El experimento NIPS y la aleatoriedad de la publicación científica

Como ya hemos hablado por aquí en anteriores posts, el proceso de publicación científica es bastante complejo. Para asegurar la calidad científica de los artículos publicados se envían antes a científicos en activo que los evalúen, en el proceso llamado peer review o publicación por pares. Estos otros científicos (referees) deben evaluar si el artículo es consistente, si es o no interesante para la comunidad y otras cuestiones. Lo que no evalúan necesariamente es si es correcto o no, ya que rehacer cálculos o experimentos es muy complicado, pero sí que pueden resaltar inconsistencias o contradicciones en el mismo paper. En los últimos años, debido a la explosión de publicaciones e investigadores, la mayoría de las revistas lo que más piden a los referees es que evalúen el interés de la publicación. Esto es un tema bastante subjetivo, y nos lleva al resultado del experimento que vamos a discutir. 

El experimento en cuestión se realizó en una conferencia NIPS (Neural Information Processing Systems Foundation). Esta es una de las conferencias más importantes de su campo, y de las más multitudinarias en todos los campos. La conferencia organiza también unas publicaciones, cosa habitual, y decidieron aprovechar estas publicaciones para analizar la aleatoriedad en el proceso de evaluación. 

El experimento se diseñó de la siguiente manera. De todos los artículos recibidos eligieron un 10% (166) al azar para realizar el estudio. Estos artículos no serían evaluados por un comité, como los demás, sino por dos comités diferentes. En realidad dividieron el comité en dos, pero viene a ser lo mismo. El comité tenía instrucciones de aceptar el 22.5% de los artículos, lo que deja aproximadamente 37 ó 38  artículos dentro del conjunto a analizar que serían aceptados. Una vez los referees evaluaron los artículos compararon los resultados de ambos comités. El resultado fue muy interesante. De los 166 papers 43 recibieron evaluaciones diferentes de los dos comités, eso quiere decir que el primer comité aceptó 21 artículos que no aceptó el segundo, mientras que el segundo aceptó 22 que no aceptó el primero. Esto supone un 25.9% de artículos en los que ambos comités difirieron. Es más impresionante aún si calculamos el porcentaje de artículos en la lista de aceptados. Dado que el primer comité tenía instrucciones de aceptar unos 37 artículos, y de los que aceptó 37 no coincidían con el segundo comité concluimos que el 21/37=56.7% de los artículos aceptados por el primer comité no serían aceptados por el segundo. Más de la mitad. En conclusión, con respecto a los artículos aceptados los comités difirieron más que coincidieron. 

El resultado es bastante impresionante. Si los comité simplemente eligieran aleatoriamente los artículos a publicar, la tasa de diferencia sería de media del 77.5%, no tan lejano al resultado obtenido. La probabilidad de que se obtuvieran estos resultados a partir de un modelo totalmente aleatorio es muy baja, como se ve en el siguiente gráfico. 

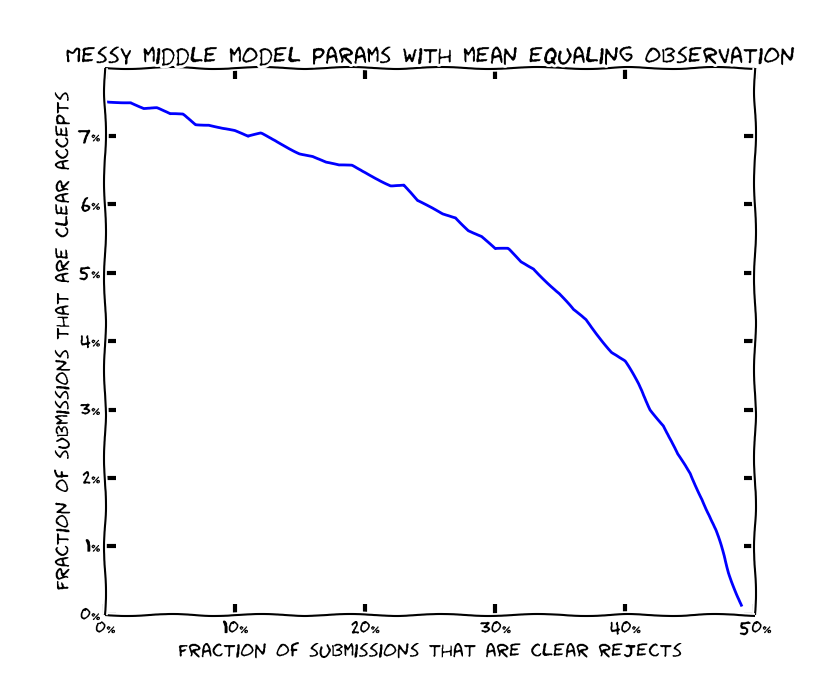
Para explicar el resultado, se pueden usar modelos más refinados. Por ejemplo, podemos suponer que X de los artículos eran claramente aceptables, e y de los artículos claramente rechazables. El resto de artículos son totalmente aleatorios. Entonces se puede calcular el porcentaje de discrepancia en función de X e Y. En esta gráfica se ven los valores de X en función de Y (o al revés) necesarios para conseguir el porcentaje del experimento.

Otro modelo más sofisticado. Supongamos que cada artículo tiene un valor 'real'. Como cada artículo es diferente podemos suponer que el valor real de cada uno es aleatorio. Supongamos también que los valores reales se distribuyen como una variable gaussiana de media 0 y varianza $\sigma_{\text{between}}$. Por supuesto, la calidad de los artículos es comparativa, por lo que el valor de la media es irrelevante. Esto nos da para cada artículo un valor real $\nu$. Ahora suponemos que la valoración de los referees es también aleatoria, siguiendo una distribución gaussiana con media en el valor real del artículo $\nu$ y varianza $\sigma_{\text{within}}$. La discrepancia entre comités vendrá dada ahora por la relación $\sigma_{\text{between}}/ \sigma_{\text{within}}$. En la siguiente gráfica se ven como se distribuye la discrepancia según este modelo para distintos valores de $\sigma_{\text{between}}/ \sigma_{\text{within}}$. El valor que maximiza la probabilidad del resultado obtenido se encuentra en $\sigma_{\text{between}}/ \sigma_{\text{within}}=1/2$. Esto viene a decir que la aleatoriedad en la evaluación debe ser bastante mayor que la aleatoriedad en la calidad real de los artículos.

Me ha parecido un experimento muy interesante. Es incuestionable que el proceso de peer review tiene mucha aleatoriedad implícita. Sin embargo, todos dependemos de él para progresar en nuestras carreras científicas. Así que la pregunta es clara: ¿Hay un método mejor?



Fuente: The Moody Road

Nota: Durante todo el post he usado dos anglicismos muy comunes en investigación.

paper <-> artículo
referee <-> evaluador